Afficher la courbe d'une fonction avec la calculatrice numworks
Saisir l'expression de la fonction
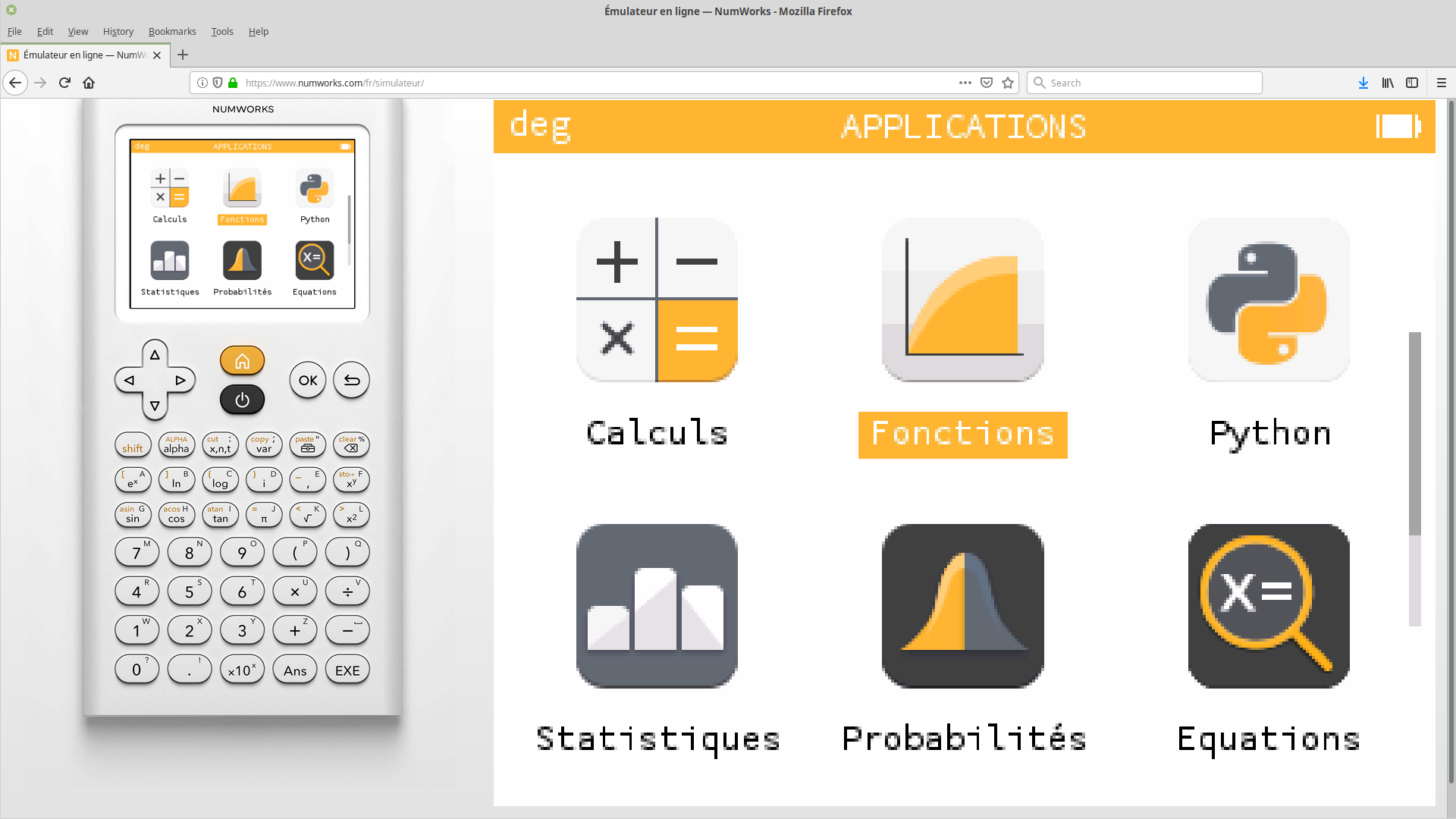
Sélectionner l'application «Fonctions».
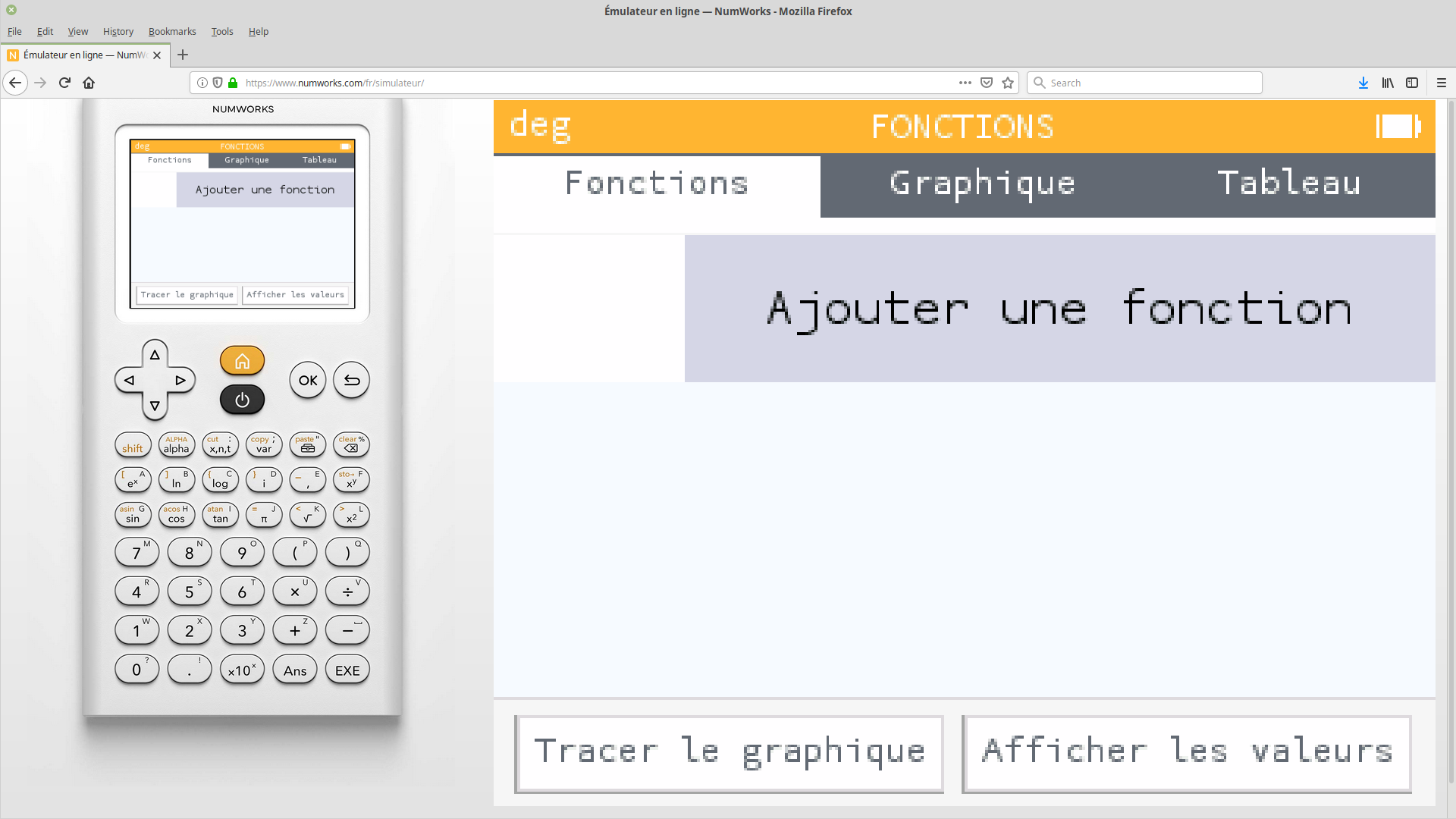
Ajouter une fonction.
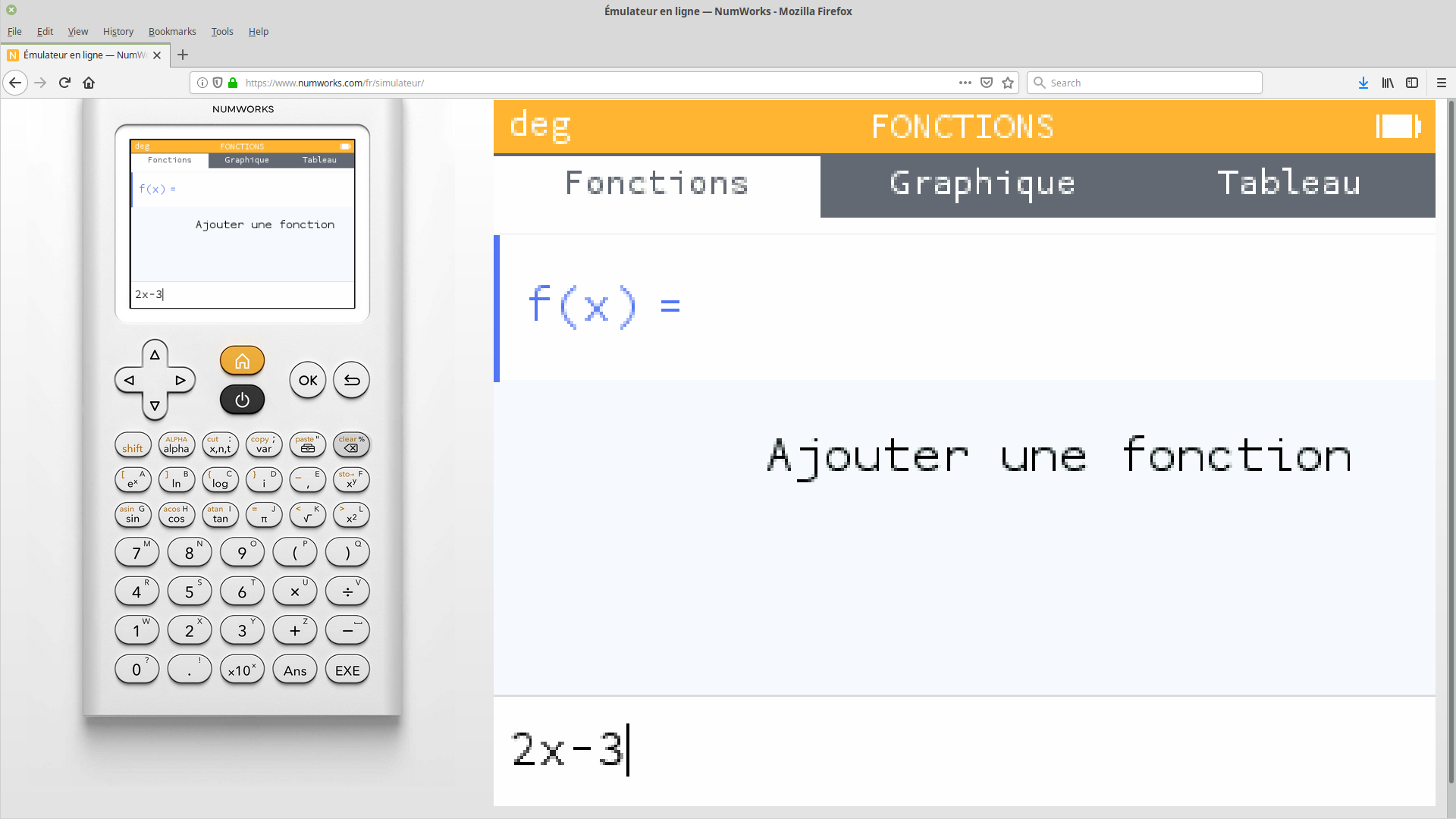
Saisir l'expression de la fonction, de variable `x`.
Dans cet exemple, on définit la fonction $f$ telle que $f(x)=3x-3.$
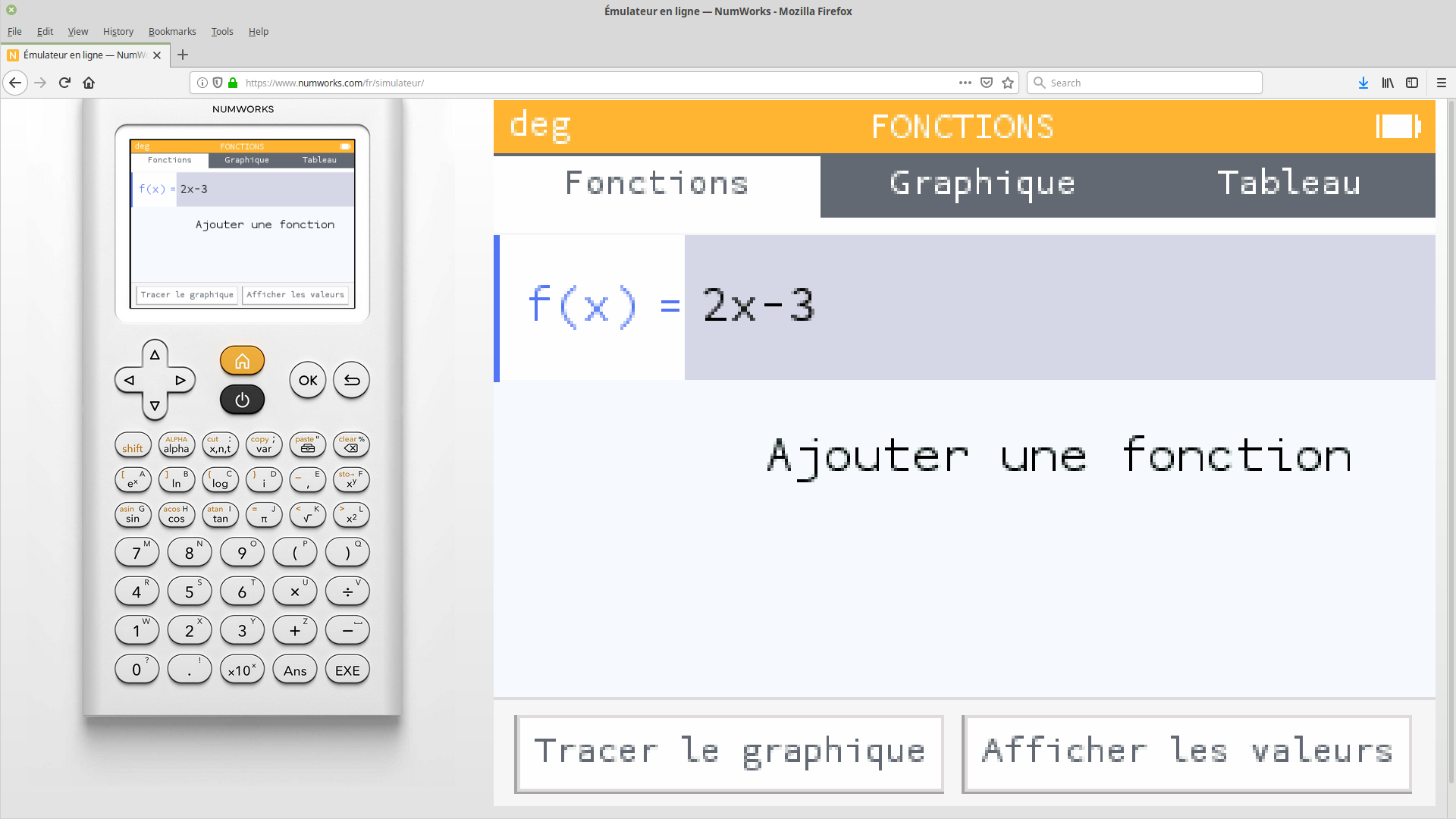
Valider la saisie, puis aller sur «Tracer le graphique, et valider de nouveau
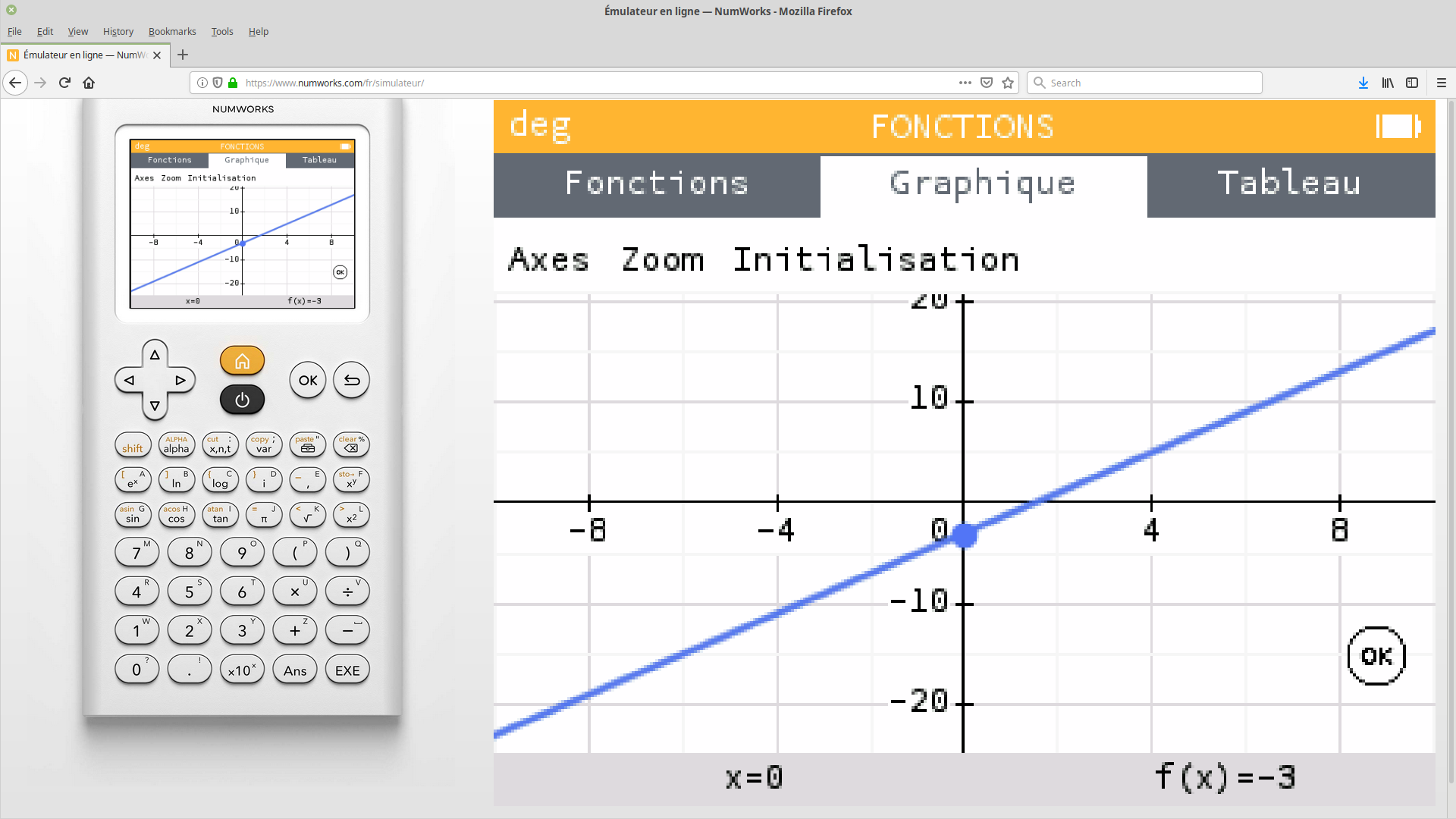
La courbe de la fonction s'affiche dans un repère prédéfini.
Manipuler l'écran graphique
Changer l'échelle des axes
Le repère est ici adapté à la fonction : il donne l'allure générale de la courbe mais n'est pas souvent adapté aux manipulations habituelles.
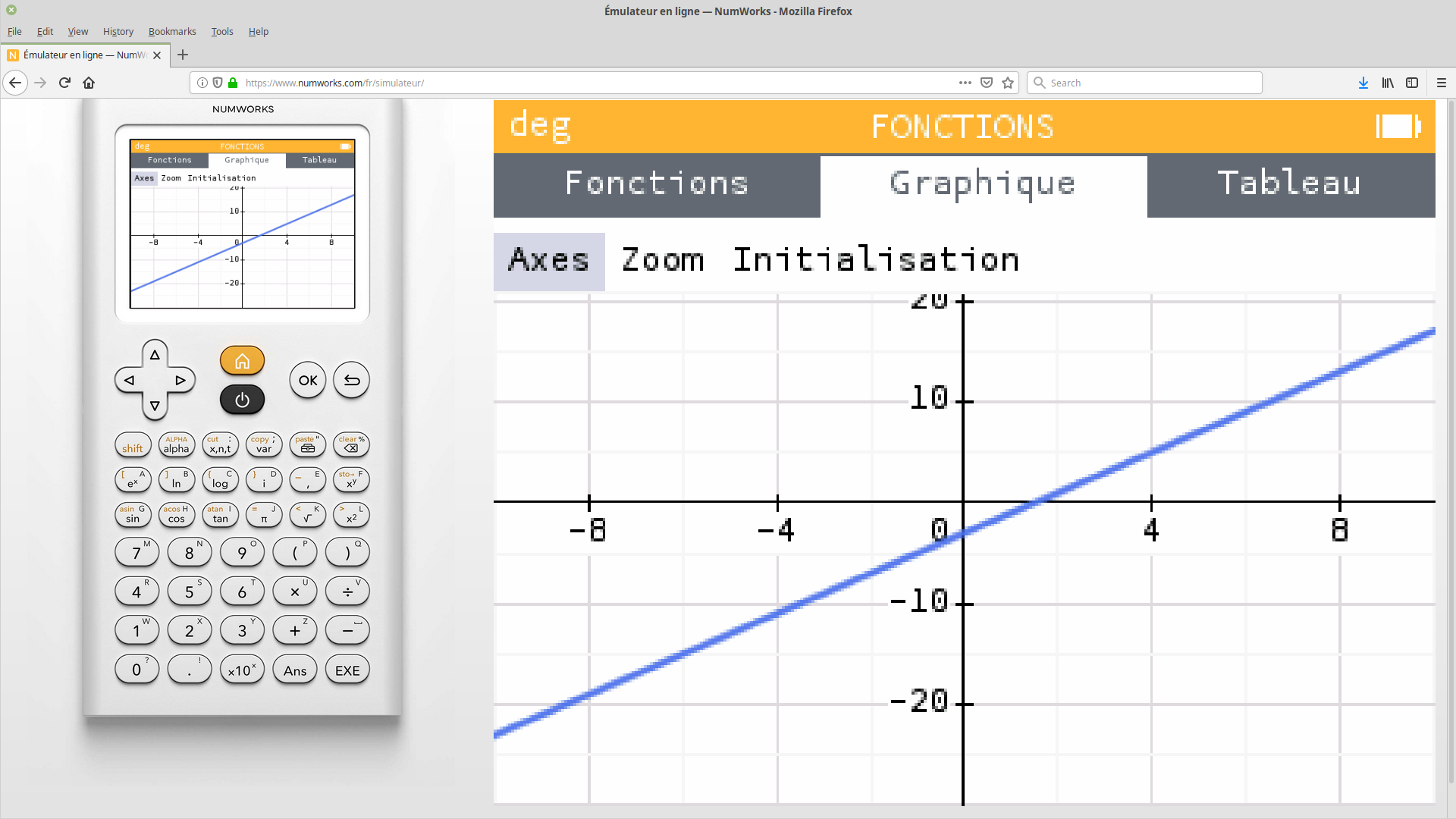
On sélectionne le menu «Axes» en haut de l'écran.
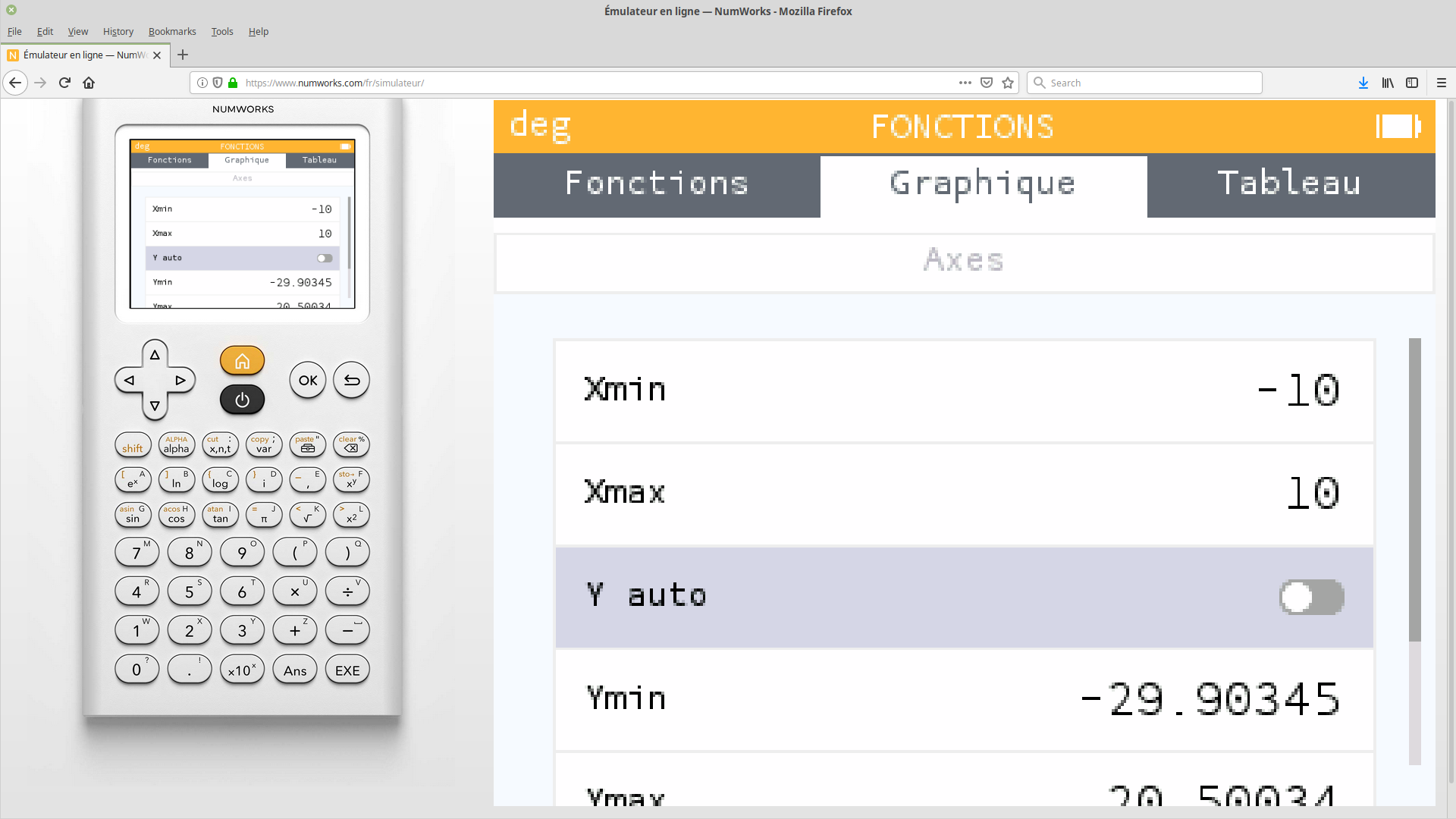
On éteint la foncion «Y Auto».
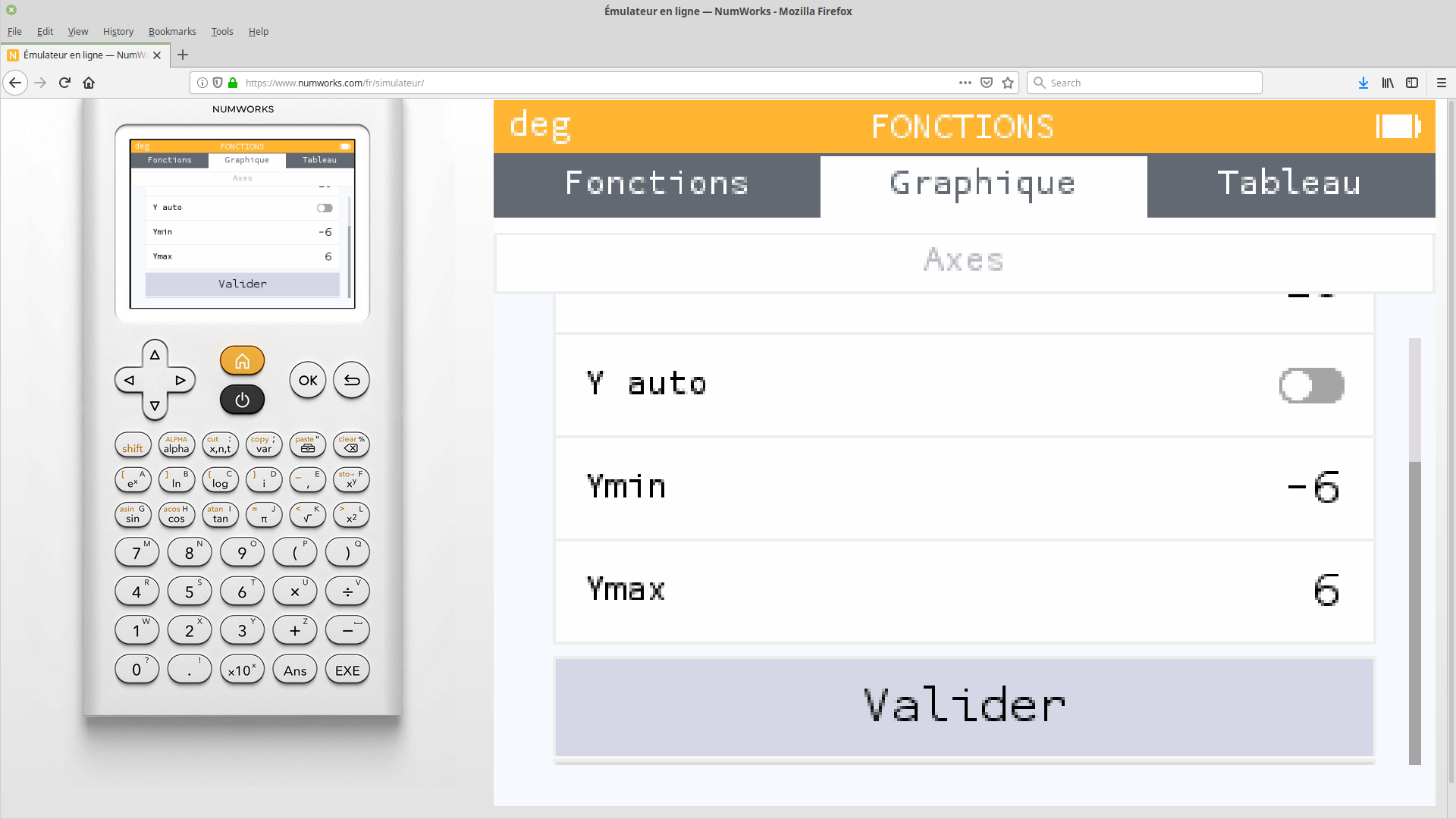
On peut ainsi changer «Ymin» et «Ymax», auxquels on affecte respectivement $-6$ et $6.$
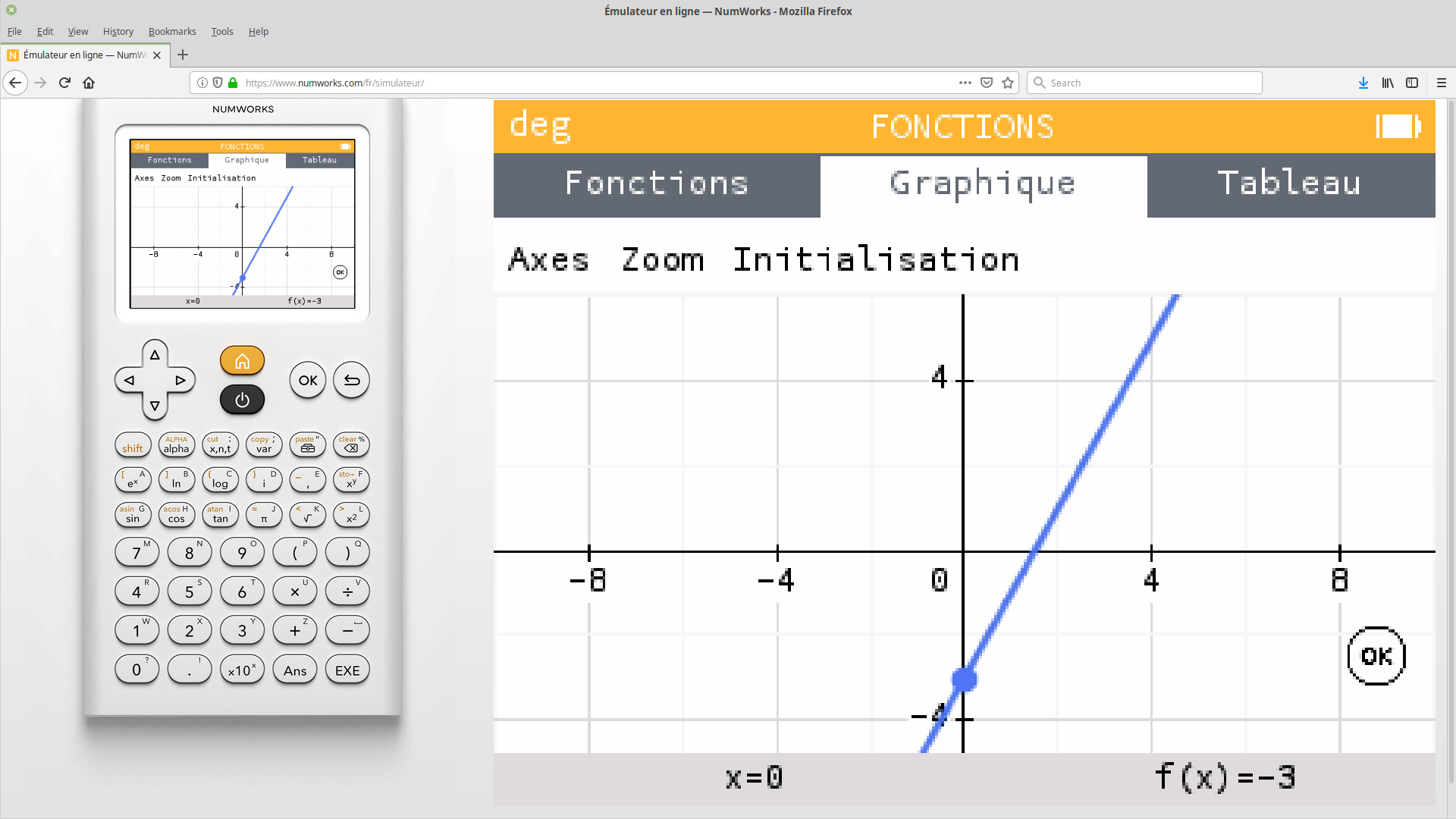
La courbe est maintenant affichée dans un repère **orthonormé**, c'est à dire que les axes des abscisses et des ordonnées ont la même échelle.
Agir sur le zoom
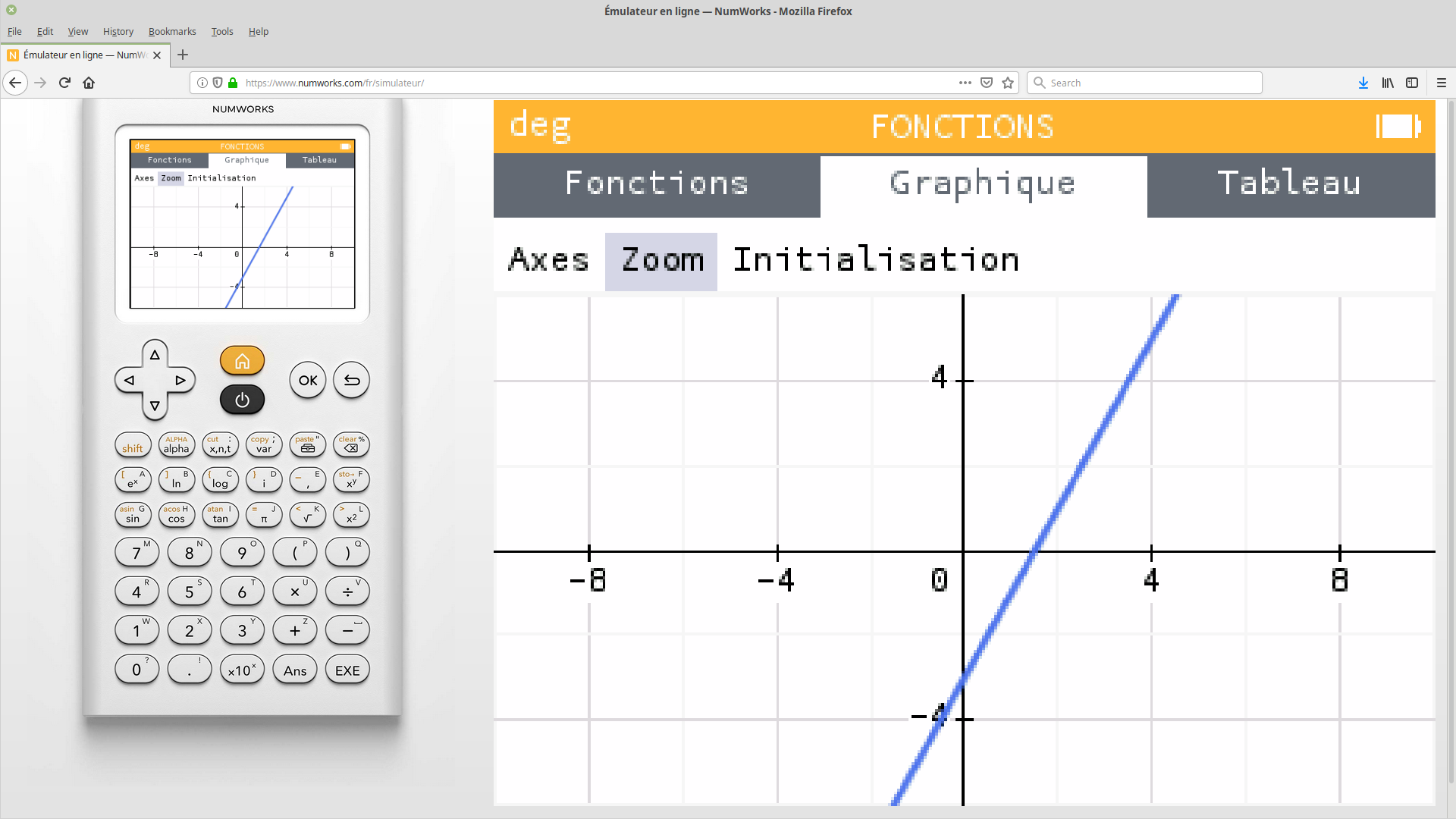
On peut ensuite déplacer la courbe, l'agrandir ou la rapetisser à l'aide du menu «Zoom», en haut de l'écran.
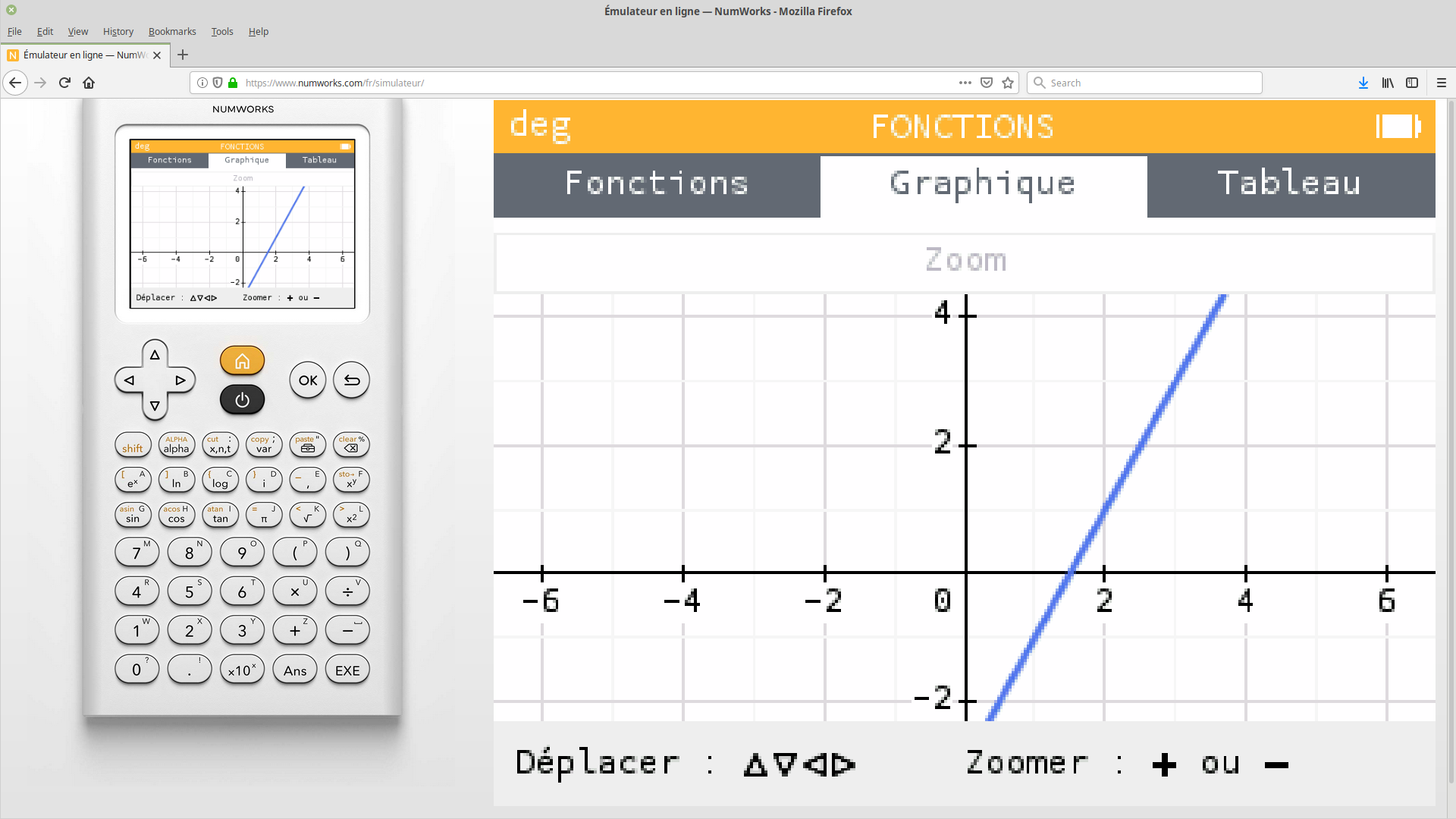
Ce menu permet d'utiliser les flèches de la calculatrice pour déplacer la courbe, et les boutons «`+`» et «`-`» pour agir sur le zoom.
Un exemple d'opération avancée
Nous allons maintenant utiliser l'une des fontions avancées accessibles par le bouton «`ok`».
Un menu apparaît. La flèche droite de la calculatrice affiche les fonctions du menu «Calculer».
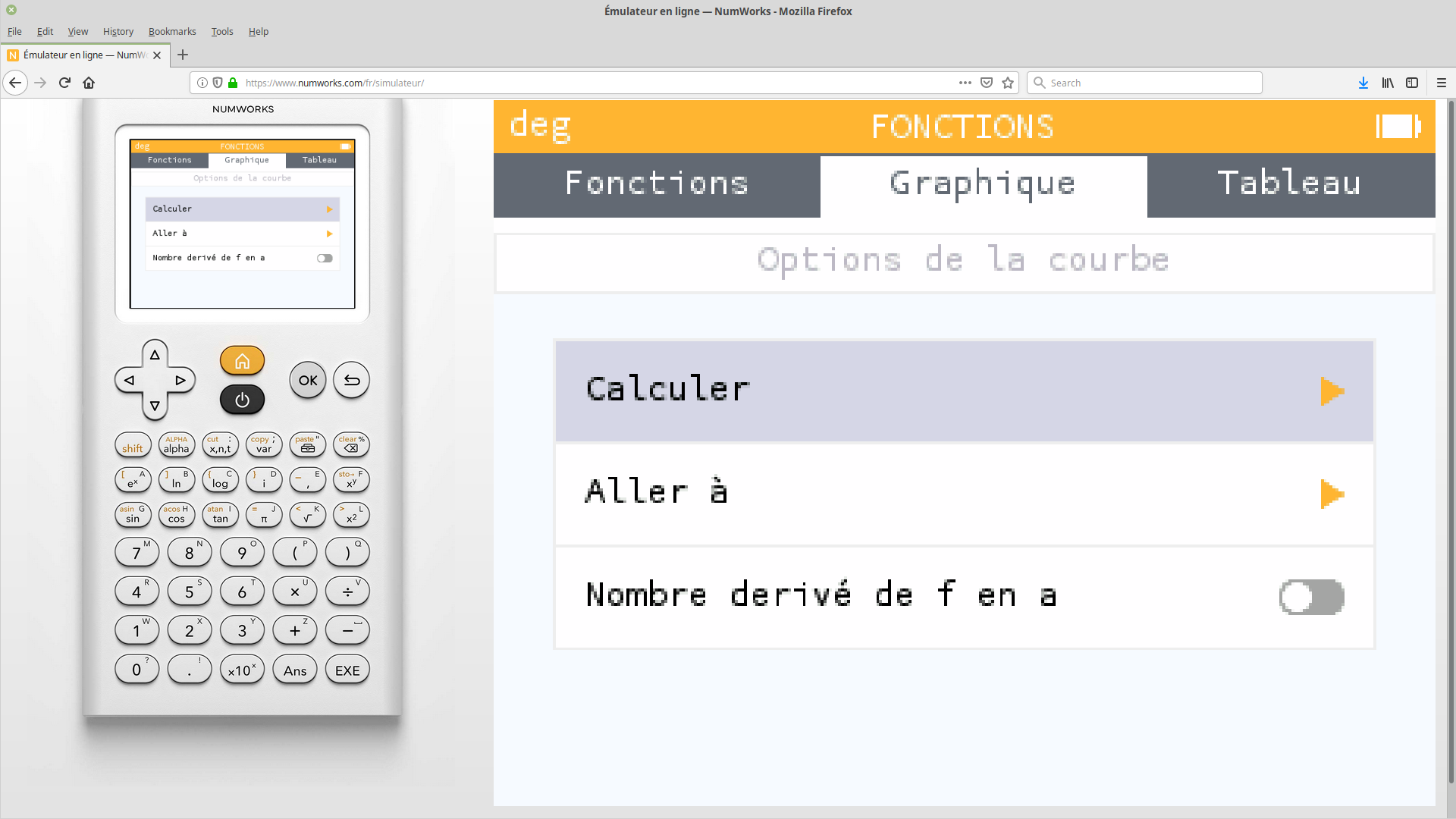
Sélectionner «Racines», puis valider.
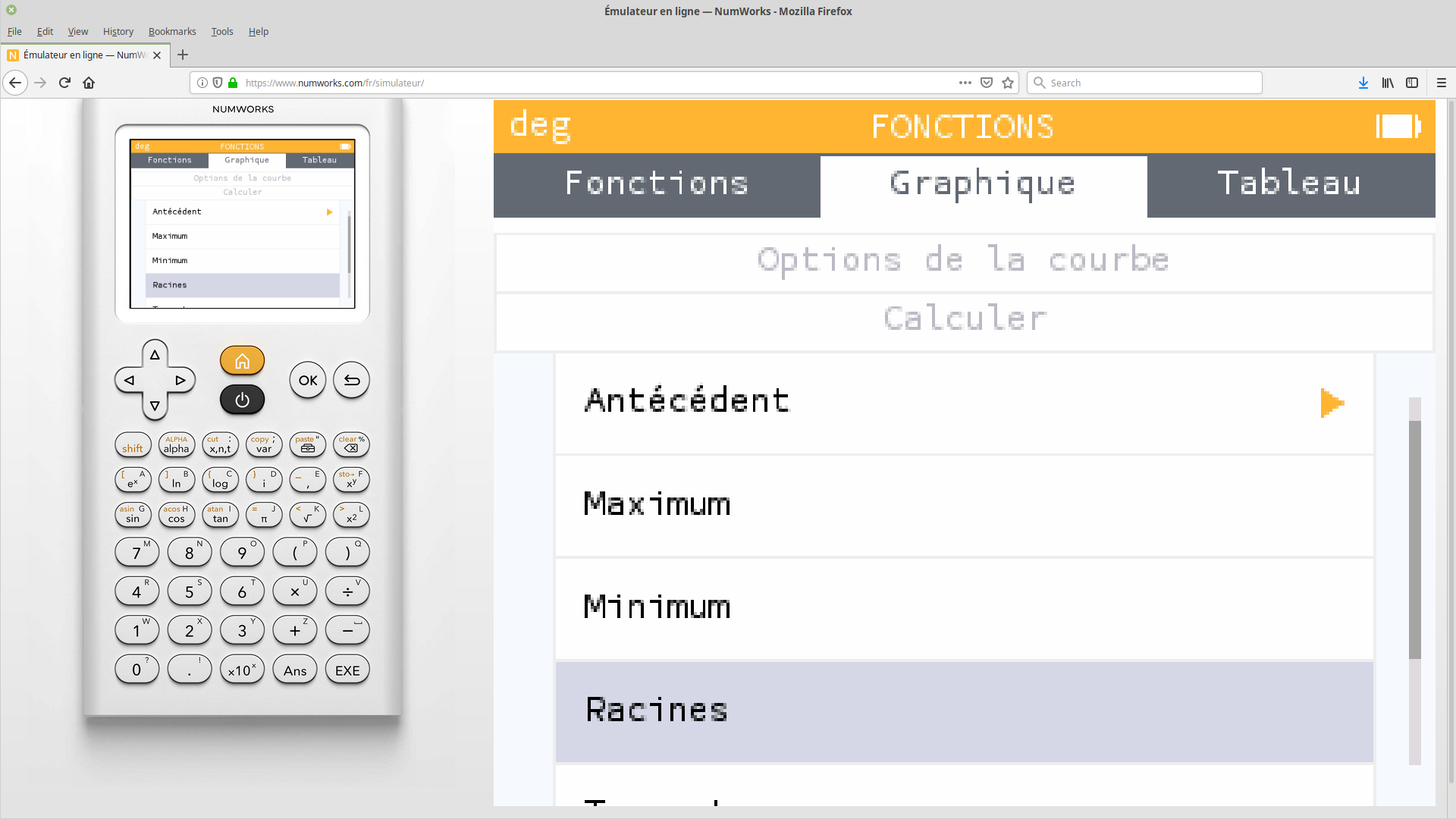
Dans le bas de l'écran, on peut maintenant lire `x=1.5 f(x)=0`.
La calculatrice a déterminé automatiquement une valeur approchée d'un `x` tel que `f(x)=0`. Ici, c'est `1.5`.
Ce résultat indique que $f(1,5)=0,$ autrement dit que $1,5$ est un antécédente de $0$ par la fonction $f$.
Obtenir un tableau de valeurs
Le menu «Tableau», en haut de l'écran, permet d'accéder à cette fonctionnalité.
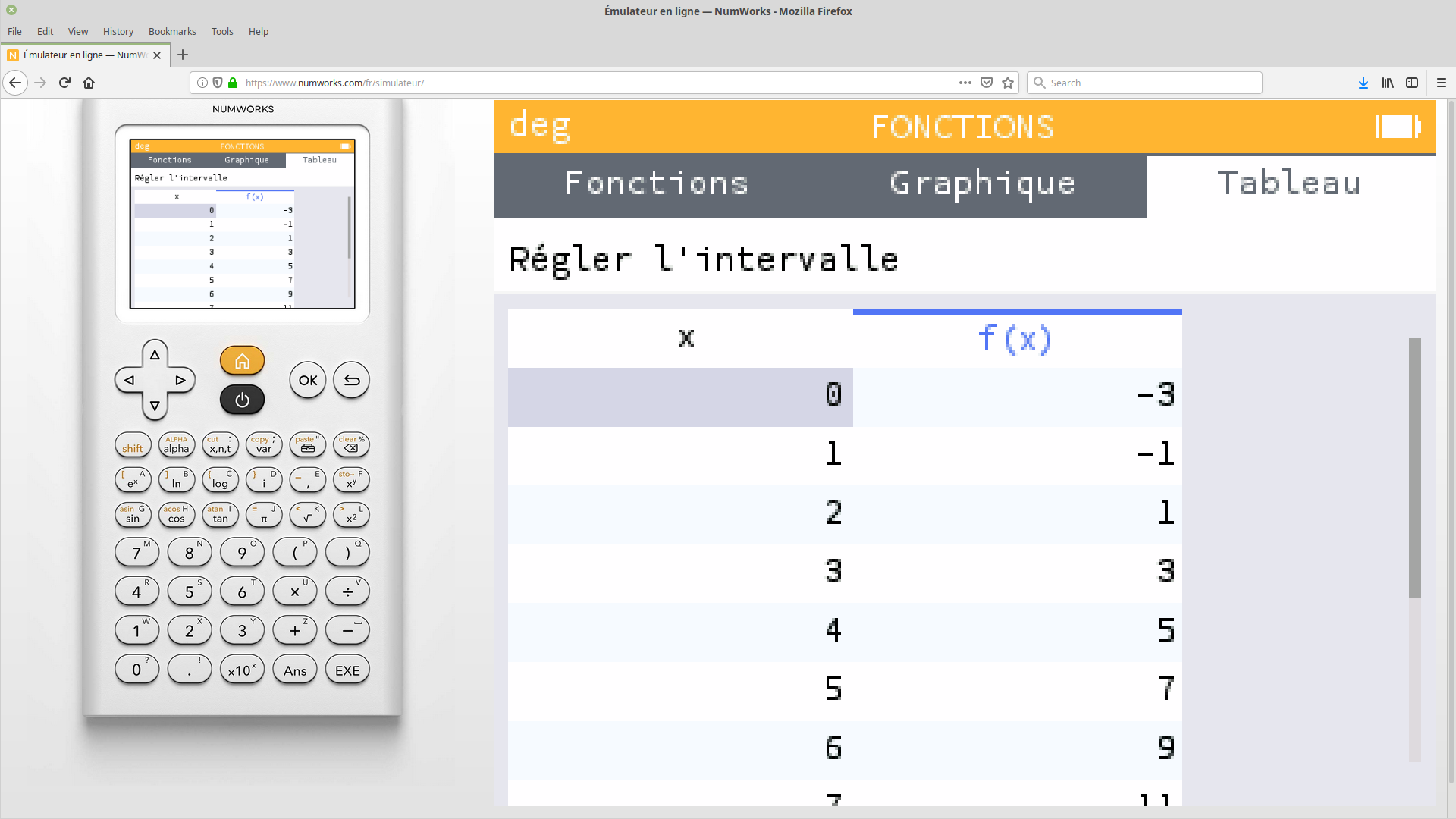
Dans le tableau affiché, on trouve dans la colonne `x` des nombres, et à droite les valeurs approchées de leurs images par la fonction $f$.
Ici, par exemple, la première ligne de ce tableau indique que lorsque $x=0$, $f(x)=-3$, autrement dit que $f(0)=-3.$